Trignometry Complex Questions

1. If cos A = 4/5 , then the value of tan A is

(A) 3/5             (B)3/4              (C)4/3              (D)5/3

2. If sin A = 1/2 , then the value of cot A is

(A) 3                (B) 1/3             (C) 3/2             (D) 1

3. The value of the expression [cosec (75° + q) – sec (15° – q – tan (55° + q+ cot (35° – q)] is

(A) – 1             (B) 0                (C) 1                (D) 3/2

4. Given that sinq= a/b , then cosq is equal to 



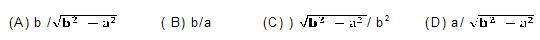
5. If cos (a + b) = 0, then sin (a - b) can be reduced to

(A) cos b                     (B) cos 2b                   (C) sin α                      (D) sin 2a

6. The value of (tan1° tan 2° tan3° ... tan 89°) is

(A) 0                (B) 1                (C) 2                            (D)1 / 2

7. If cos 9a= sinα and 9a < 90°, then the value of tan5a is

(A) 1/√3                       (B) √ 3                         (C) 1                (D) 0

8. If DABC is right angled at C, then the value of cos (A+B) is

(A) 0                (B) 1                            (C) 1/2                         (D)√3/2

9. If sinA + sin²A = 1, then the value of the expression (cos²A + cos⁴A) is

(A) 1                (B) 1/2                         (C) 2                            (D) 3

10. Given that sina= 1/2 and cosb =1/2 , then the value of (a + b) is

(A) 0°                           (B) 30°                         (C) 60°            (D) 90°

11. The value of the expression [sin² 22⁰ sin² 68⁰ / cos² 22⁰ cos² 68⁰       +  sin ² 63⁰ cos  63⁰ sin 27⁰ ]   is         

(A) 3                (B) 2                (C) 1                            (D) 0

12. If 4 tanq = 3, then [4sinq - cosq ] / [4sinq + cos q ] is equal to

(A) 2/3                                     (B) 1/3                         (C) 1/2             (D) 3/4

13. If sinq – cosq = 0, then the value of (sin⁴q + cos⁴qθ) is

(A) 1                (B) 3/4                         (C) 1/2                         (D) 1/4

14. sin (45° + q) – cos (45° – q) is equal to

(A) 2cosq                    (B) 0                (C) 2 sin q                   (D) 1

15. A pole 6 m high casts a shadow 2 √3m long on the ground, then the Sun’s elevation is

(A\) 60°                        (B) 45°                         (C) 30°                        (D) 90°

Exercise 5.1

Exercise 5.1

Question 1:

In which of the following situations, does the list of numbers involved make as arithmetic progression and why?

(i) The taxi fare after each km when the fare is Rs 15 for the first km and Rs 8 for each additional km.

(ii) The amount of air present in a cylinder when a vacuum pump removesof the air remaining in the cylinder at a time.

(iii) The cost of digging a well after every metre of digging, when it costs Rs 150 for the first metre and rises by Rs 50 for each subsequent metre.

(iv)The amount of money in the account every year, when Rs 10000 is deposited at compound interest at 8% per annum.

(i) It can be observed that
Taxi fare for 1^st km = 15
Taxi fare for first 2 km = 15 + 8 = 23
Taxi fare for first 3 km = 23 + 8 = 31
Taxi fare for first 4 km = 31 + 8 = 39
Clearly 15, 23, 31, 39 … forms an A.P. because every term is 8 more than the preceding term.
(ii) Let the initial volume of air in a cylinder be V lit. In each stroke, the vacuum pump removes of air remaining in the cylinder at a time. In other words, after every stroke, only part of air will remain.
Therefore, volumes will be 
Clearly, it can be observed that the adjacent terms of this series do not have the same difference between them. Therefore, this is not an A.P.
(iii) Cost of digging for first metre = 150
Cost of digging for first 2 metres = 150 + 50 = 200
Cost of digging for first 3 metres = 200 + 50 = 250
Cost of digging for first 4 metres = 250 + 50 = 300
Clearly, 150, 200, 250, 300 … forms an A.P. because every term is 50 more than the preceding term.
(iv) We know that if Rs P is deposited at r% compound interest per annum for n years, our money will be after n years.
Therefore, after every year, our money will be

Clearly, adjacent terms of this series do not have the same difference between them. Therefore, this is not an A.P.

Question 2:

Write first four terms of the A.P. when the first term a and the common difference d are given as follows

(i) a = 10, d = 10

(ii) a = − 2, d = 0

(iii) a = 4, d = − 3

(iv) a = − 1 d = 

(v) a = − 1.25, d = − 0.25

(i) a = 10, d = 10
Let the series be a₁, a₂, a₃, a₄, a₅ …
a₁ = a = 10
a₂ = a₁ + d = 10 + 10 = 20
a₃ = a₂ + d = 20 + 10 = 30
a₄ = a₃ + d = 30 + 10 = 40
a₅ = a₄ + d = 40 + 10 = 50
Therefore, the series will be 10, 20, 30, 40, 50 …
First four terms of this A.P. will be 10, 20, 30, and 40.
(ii) a = −2, d = 0
Let the series be a₁, a₂, a₃, a₄ …
a₁ = a = −2
a₂ = a₁ + d = − 2 + 0 = −2
a₃ = a₂ + d = − 2 + 0 = −2
a₄ = a₃ + d = − 2 + 0 = −2
Therefore, the series will be −2, −2, −2, −2 …
First four terms of this A.P. will be −2, −2, −2 and −2.
(iii) a = 4, d = −3
Let the series be a₁, a₂, a₃, a₄ …
a₁ = a = 4
a₂ = a₁ + d = 4 − 3 = 1
a₃ = a₂ + d = 1 − 3 = −2
a₄ = a₃ + d = − 2 − 3 = −5
Therefore, the series will be 4, 1, −2 −5 …
First four terms of this A.P. will be 4, 1, −2 and −5.
(iv) a = −1, d = 
Let the series be a₁, a₂, a₃, a₄ …

Clearly, the series will be
 ………….
First four terms of this A.P. will be .
(v) a = −1.25, d = −0.25
Let the series be a₁, a₂, a₃, a₄ …
a₁ = a = −1.25
a₂ = a₁ + d = − 1.25 − 0.25 = −1.50
a₃ = a₂ + d = − 1.50 − 0.25 = −1.75
a₄ = a₃ + d = − 1.75 − 0.25 = −2.00
Clearly, the series will be 1.25, −1.50, −1.75, −2.00 ……..
First four terms of this A.P. will be −1.25, −1.50, −1.75 and −2.00.

Question 3:

For the following A.P.s, write the first term and the common difference.

(i) 3, 1, − 1, − 3 …

(ii) − 5, − 1, 3, 7 …

(iii) 

(iv) 0.6, 1.7, 2.8, 3.9 …

(i) 3, 1, −1, −3 …
Here, first term, a = 3
Common difference, d = Second term − First term
= 1 − 3 = −2
(ii) −5, −1, 3, 7 …
Here, first term, a = −5
Common difference, d = Second term − First term
= (−1) − (−5) = − 1 + 5 = 4
(iii) 
Here, first term, 
Common difference, d = Second term − First term

(iv) 0.6, 1.7, 2.8, 3.9 …
Here, first term, a = 0.6
Common difference, d = Second term − First term
= 1.7 − 0.6
= 1.1

Question 4:

Which of the following are APs? If they form an A.P. find the common difference d and write three more terms.

(i) 2, 4, 8, 16 …

(ii) 

(iii) − 1.2, − 3.2, − 5.2, − 7.2 …

(iv) − 10, − 6, − 2, 2 …

(v) 

(vi) 0.2, 0.22, 0.222, 0.2222 ….

(vii) 0, − 4, − 8, − 12 …

(viii) 

(ix) 1, 3, 9, 27 …

(x) a, 2a, 3a, 4a …

(xi) a, a², a³, a⁴ …
(xii) 

(xiii) 

(xiv) 1², 3², 5², 7² …

(xv) 1², 5², 7², 73 …

(i) 2, 4, 8, 16 …
It can be observed that
a₂ − a₁ = 4 − 2 = 2
a₃ − a₂ = 8 − 4 = 4
a₄ − a₃ = 16 − 8 = 8
i.e., a_k+1− a_k is not the same every time. Therefore, the given numbers are not forming an A.P.
(ii) 
It can be observed that

i.e., a_k+1− a_k is same every time.
Therefore,  and the given numbers are in A.P.
Three more terms are

(iii) −1.2, −3.2, −5.2, −7.2 …
It can be observed that
a₂ − a₁ = (−3.2) − (−1.2) = −2
a₃ − a₂ = (−5.2) − (−3.2) = −2
a₄ − a₃ = (−7.2) − (−5.2) = −2
i.e., a_k+1− a_k is same every time. Therefore, d = −2
The given numbers are in A.P.
Three more terms are
a₅ = − 7.2 − 2 = −9.2
a₆ = − 9.2 − 2 = −11.2
a₇ = − 11.2 − 2 = −13.2
(iv) −10, −6, −2, 2 …
It can be observed that
a₂ − a₁ = (−6) − (−10) = 4
a₃ − a₂ = (−2) − (−6) = 4
a₄ − a₃ = (2) − (−2) = 4
i.e., a_k+1 − a_k is same every time. Therefore, d = 4
The given numbers are in A.P.
Three more terms are
a₅ = 2 + 4 = 6
a₆ = 6 + 4 = 10
a₇ = 10 + 4 = 14
(v) 
It can be observed that

i.e., a_{k+1 −} a_k is same every time. Therefore, 
The given numbers are in A.P.
Three more terms are

(vi) 0.2, 0.22, 0.222, 0.2222 ….
It can be observed that
a₂ − a₁ = 0.22 − 0.2 = 0.02
a₃ − a₂ = 0.222 − 0.22 = 0.002
a₄ − a₃ = 0.2222 − 0.222 = 0.0002
i.e., a_k+1 − a_k is not the same every time.
Therefore, the given numbers are not in A.P.
(vii) 0, −4, −8, −12 …
It can be observed that
a₂ − a₁ = (−4) − 0 = −4
a₃ − a₂ = (−8) − (−4) = −4
a₄ − a₃ = (−12) − (−8) = −4
i.e., a_k+1 − a_k is same every time. Therefore, d = −4
The given numbers are in A.P.
Three more terms are
a₅ = − 12 − 4 = −16
a₆ = − 16 − 4 = −20
a₇ = − 20 − 4 = −24
(viii) 
It can be observed that

i.e., a_k+1 − a_k is same every time. Therefore, d = 0
The given numbers are in A.P.
Three more terms are

(ix) 1, 3, 9, 27 …
It can be observed that
a₂ − a₁ = 3 − 1 = 2
a₃ − a₂ = 9 − 3 = 6
a₄ − a₃ = 27 − 9 = 18
i.e., a_k+1 − a_k is not the same every time.
Therefore, the given numbers are not in A.P.
(x) a, 2a, 3a, 4a …
It can be observed that
a₂ − a₁ = 2a − a = a
a₃ − a₂ = 3a − 2a = a
a₄ − a₃ = 4a − 3a = a
i.e., a_k+1 − a_k is same every time. Therefore, d = a
The given numbers are in A.P.
Three more terms are
a₅ = 4a + a = 5a
a₆ = 5a + a = 6a
a₇ = 6a + a = 7a
(xi) a, a², a³, a⁴ …
It can be observed that
a₂ − a₁ = a² − a = a (a − 1)
a₃ − a₂ = a³ − a² = a² (a − 1)
a₄ − a₃ = a⁴ − a³ = a³ (a − 1)
i.e., a_k+1 − a_k is not the same every time.
Therefore, the given numbers are not in A.P.
(xii) 
It can be observed that

i.e., a_k+1 − a_k is same every time.
Therefore, the given numbers are in A.P.
And, 
Three more terms are

(xiii) 
It can be observed that

i.e., a_k+1 − a_k is not the same every time.
Therefore, the given numbers are not in A.P.
(xiv) 1², 3², 5², 7² …
Or, 1, 9, 25, 49 …..
It can be observed that
a₂ − a₁ = 9 − 1 = 8
a₃ − a₂ = 25 − 9 = 16
a₄ − a₃ = 49 − 25 = 24
i.e., a_k+1 − a_k is not the same every time.
Therefore, the given numbers are not in A.P.
(xv) 1², 5², 7², 73 …
Or 1, 25, 49, 73 …
It can be observed that
a₂ − a₁ = 25 − 1 = 24
a₃ − a₂ = 49 − 25 = 24
a₄ − a₃ = 73 − 49 = 24
i.e., a_k+1 − a_k is same every time.
Therefore, the given numbers are in A.P.
And, d = 24
Three more terms are
a₅ = 73+ 24 = 97
a₆ = 97 + 24 = 121
a₇ = 121 + 24 = 145

Exercise 4.4

Exercise 4.4

Question 1:

Find the nature of the roots of the following quadratic equations.
If the real roots exist, find them;
(I) 2x² −3x + 5 = 0
(II) 
(III) 2x² − 6x + 3 = 0

We know that for a quadratic equation ax² + bx + c = 0, discriminant is b² − 4ac.
(A) If b² − 4ac > 0 → two distinct real roots
(B) If b² − 4ac = 0 → two equal real roots
(C) If b² − 4ac < 0 → no real roots
(I) 2x² −3x + 5 = 0
Comparing this equation with ax² + bx + c = 0, we obtain
a = 2, b = −3, c = 5
Discriminant = b² − 4ac = (− 3)² − 4 (2) (5) = 9 − 40
= −31
As b² − 4ac < 0,
Therefore, no real root is possible for the given equation.
(II) 
Comparing this equation with ax² + bx + c = 0, we obtain

Discriminant 
= 48 − 48 = 0
As b² − 4ac = 0,
Therefore, real roots exist for the given equation and they are equal to each other.
And the roots will be and .

Therefore, the roots are and.
(III) 2x² − 6x + 3 = 0
Comparing this equation with ax² + bx + c = 0, we obtain
a = 2, b = −6, c = 3
Discriminant = b² − 4ac = (− 6)² − 4 (2) (3)
= 36 − 24 = 12
As b² − 4ac > 0,
Therefore, distinct real roots exist for this equation as follows.

Therefore, the roots are or .

Question 2:

Find the values of k for each of the following quadratic equations, so that they have two equal roots.
(I) 2x² + kx + 3 = 0
(II) kx (x − 2) + 6 = 0

We know that if an equation ax² + bx + c = 0 has two equal roots, its discriminant
(b² − 4ac) will be 0.
(I) 2x² + kx + 3 = 0
Comparing equation with ax² + bx + c = 0, we obtain
a = 2, b = k, c = 3
Discriminant = b² − 4ac = (k)²− 4(2) (3)
= k² − 24
For equal roots,
Discriminant = 0
k² − 24 = 0
k² = 24

(II) kx (x − 2) + 6 = 0
or kx² − 2kx + 6 = 0
Comparing this equation with ax² + bx + c = 0, we obtain
a = k, b = −2k, c = 6
Discriminant = b² − 4ac = (− 2k)² − 4 (k) (6)
= 4k² − 24k
For equal roots,
b² − 4ac = 0
4k² − 24k = 0
4k (k − 6) = 0
Either 4k = 0 or k = 6 = 0
k = 0 or k = 6
However, if k = 0, then the equation will not have the terms ‘x²’ and ‘x’.
Therefore, if this equation has two equal roots, k should be 6 only.

Question 3:

Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 m²?
If so, find its length and breadth.

Let the breadth of mango grove be l.
Length of mango grove will be 2l.
Area of mango grove = (2l) (l)
= 2l²

Comparing this equation with al² + bl + c = 0, we obtain
a = 1 b = 0, c = 400
Discriminant = b² − 4ac = (0)² − 4 × (1) × (− 400) = 1600
Here, b² − 4ac > 0
Therefore, the equation will have real roots. And hence, the desired rectangular mango grove can be designed.

However, length cannot be negative.
Therefore, breadth of mango grove = 20 m
Length of mango grove = 2 × 20 = 40 m

Question 4:

Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.

Let the age of one friend be x years.
Age of the other friend will be (20 − x) years.
4 years ago, age of 1^st friend = (x − 4) years
And, age of 2^nd friend = (20 − x − 4)
= (16 − x) years
Given that,
(x − 4) (16 − x) = 48
16x − 64 − x² + 4x = 48
− x² + 20x − 112 = 0
x² − 20x + 112 = 0
Comparing this equation with ax² + bx + c = 0, we obtain
a = 1, b = −20, c = 112
Discriminant = b² − 4ac = (− 20)² − 4 (1) (112)
= 400 − 448 = −48
As b² − 4ac < 0,
Therefore, no real root is possible for this equation and hence, this situation is not possible.

Question 5:

Is it possible to design a rectangular park of perimeter 80 and area 400 m²? If so find its length and breadth.

Let the length and breadth of the park be l and b.
Perimeter = 2 (l + b) = 80
l + b = 40
Or, b = 40 − l
Area = l × b = l (40 − l) = 40l − l²
40l − l² = 400
l² − 40l + 400 = 0
Comparing this equation with
al² + bl + c = 0, we obtain
a = 1, b = −40, c = 400
Discriminate = b² − 4ac = (− 40)² −4 (1) (400)
= 1600 − 1600 = 0
As b² − 4ac = 0,
Therefore, this equation has equal real roots. And hence, this situation is possible.
Root of this equation,

Therefore, length of park, l = 20 m
And breadth of park, b = 40 − l = 40 − 20 = 20